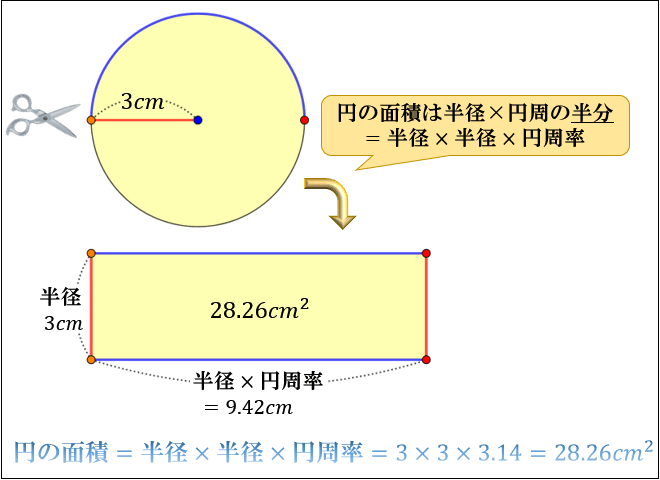
カテゴリ一覧 他の勉強がしたい方はこちら 構造力学の基礎; だからこの長方形の面積は 半径 × 半径 × π = 円の面積 で、 これは、元の円の面積と等しいよ ここまでしっかり押さえておけば、公式は忘れても求められるし どんな問題の聞き方をされても大丈夫だし、応用問題にも対抗できるよ中空円の面積の求め方はS=π÷4((外円の直径×外円の直径)(内円の直径×内円の直径))だと思うのですが、中空円柱では÷4が無いのはなぜでしょうか? keisanより 円の直径 = 2 * 円の半径 より、 円の直径 2 = 4 * 円の半径 2 となるからだと考えられます。

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
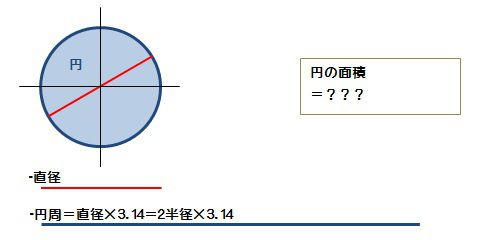
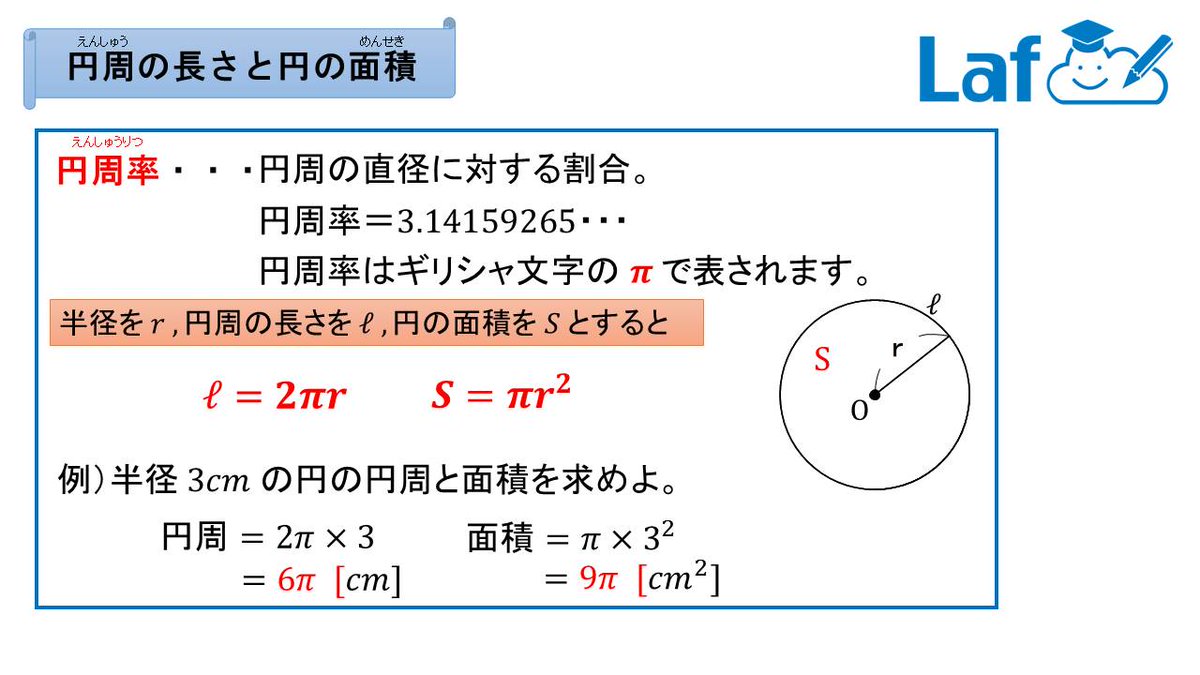
円の面積の求め方 π
円の面積の求め方 π-円で平行四辺形を作成することができるでしょうか? と、考える前に今回の挑戦に必要となる式を1つ紹介します。 円の直径と円周の関係です。 円周=直径×3.14 この3.14とはπ(パイ)と呼ばれる 円周の求め方・円周率とは何か・なぜ無限に続くのかを説明。 ですから、円の直径(2r)に円周率(π≒314)をかけることで円周の長さ(2πr ≒ 628r)が求まります。 例題①:半径5cmの円の、円周の長さを求めて下さい。




Excel エクセルで円の面積から直径を計算したり 直径から面積を求める方法 Pi関数の使用方法
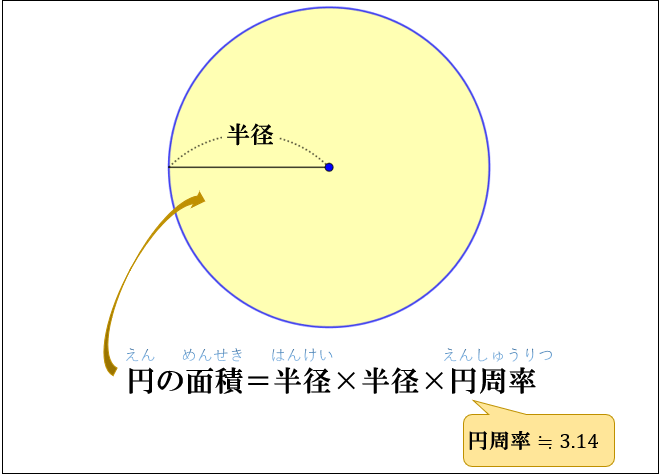
円の面積は、 「半径 × 半径 × 314」 (半径 × 半径 × 円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 答え: 2 × 2 × 314 = 1256 (cm 2) 正確には 2 × 2 × π = 4 π神官アハメスが書き残したリンド・パピルスには、円積問題の古典的な解法の一つが記されており、円の直径からその 1 / 9 を引いた長さを一辺とする正方形の面積と、元の円の面積が等しいとしている 。この計算から円周率を計算すると、 256 / 81 =直径、円の面積の詳細は下記が参考になります。 円の直径、円周とは?1分でわかる意味、円周や断面積から半径、直径を求める 円の断面積は?1分でわかる意味、公式、計算方法と求め方、直径との関係 100円から読める!ネット不要!
円錐の表面積の公式を使うのもokですが、ここでは定石通り、底面積と側面積を求めてから円錐の表面積を求めてみます。 まず、 底面積 =3 2 π =9π・・・① ですね。 次に、側面積を求めます。まず、円錐の展開図を考えて、下の図におけるlを求めます。採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く円の面積は 半径×半径×円周率 なので、上下の円の面積を求め 円の面積=4cm×4cm×π=16πcm 2 円の円周=4cm×2×π=8πcm 側面の面積=6cm×8πcm=48πcm 2 解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。
うか。ここでは面積の計算を通して数値積分のやり方を検討してみましょう。 まず、円の面積を求めることを考えます。半径を1とすると、小学校や中学校では 円周率に半径の二乗をかけてπ・1 2 つまりπという結果が教えられπ(パイ)を使って円周と円の面積をあらわす方法 小学校のときは、円の周りの長さ(円周)は、 円の直径×円周率 、円の面積は、 半径×半径×円周率 でもとめていましたね。円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ
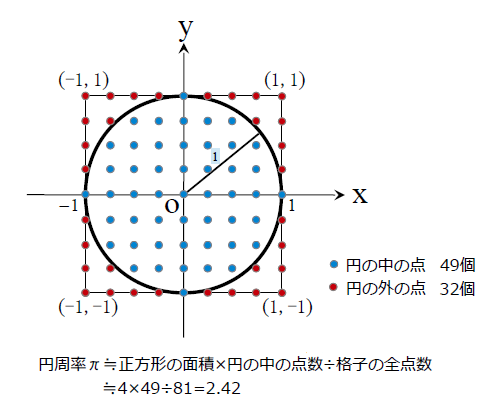



格子座標から円周率pを計算 ゆるゆるプログラミング




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube
電卓の使い方 面積を求める円の半径を入力して「計算」ボタンを押してください。 円周率は変更できます。 円周率で「πを使う」にチェックを入れると円周率をπとして計算します。 面積を入力して「計算」ボタンを押すと円の半径が計算されます この記事では、エクセルで円周率(314)の入れ方と、パイ( π )を使ったの面積を求める計算や円周の長さを求める計算について解決します。 エクセルで円の面積を求めたり、円周の長さを求める計算って、円周率( π )を使う必要があってよく解りませんよね。 ここではこんなことを紹介しています↓ 円の面積の公式はなぜ「\\(π\\)×\\(r\\)×\\(r\\)」と表現できるのでしょうか? ここではそんな疑問に対して、図形を使った簡単な公式のイメージ方法を紹介します。 先に言っておくと、ここで紹介する方法は円の面積の厳密な証明方法ではありません




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
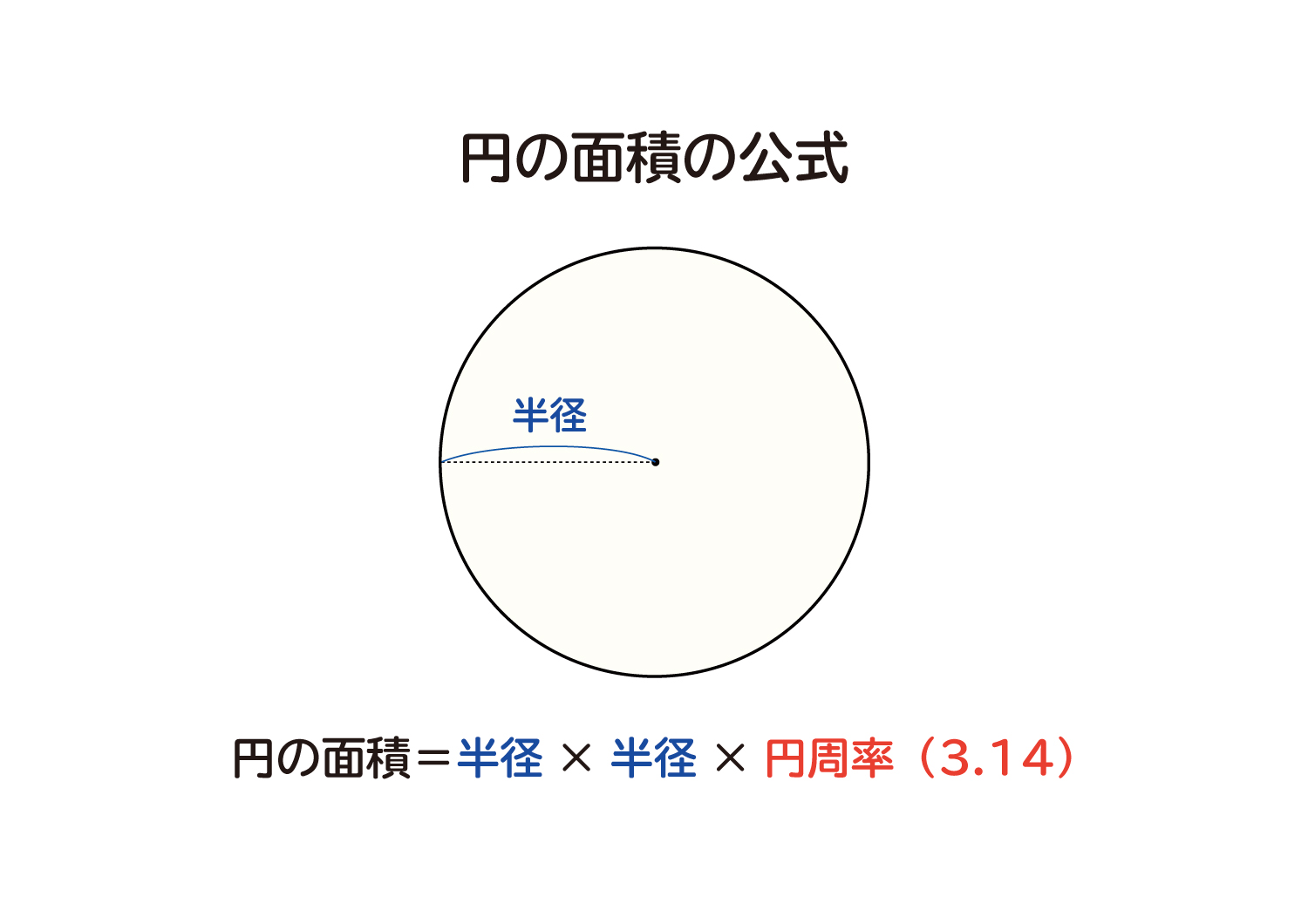



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル
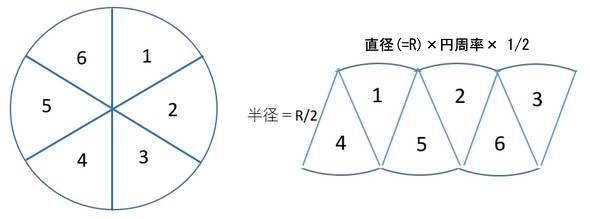
12 円の面積の公式{その1{まず,円の面積の公式について考察してみる.円周率の定義によって,半径rの 円の周の長さは2ˇr である.その円の面積はˇr2 で与えられることは,次のよう に説明されている.円周を2n等分する.これを2n個の扇形に切って,それを2つ 円周の長さは直径のπ(パイ)倍である ってことが言えるね^^ まとめ:円周率は「円周と直径の比」である 円周率の意味についてちょっとスッキリしたかな?? 次回はいよいよ円の面積・円周の長さの求め方についてみていこう。 そんじゃねー Ken円周(Circumference)から面積を計算する 円周から面積を求めるには 円周 ÷ π ÷ 2 で半径(r)を求め、 半径(r) × 半径(r) × π で求めることができます。
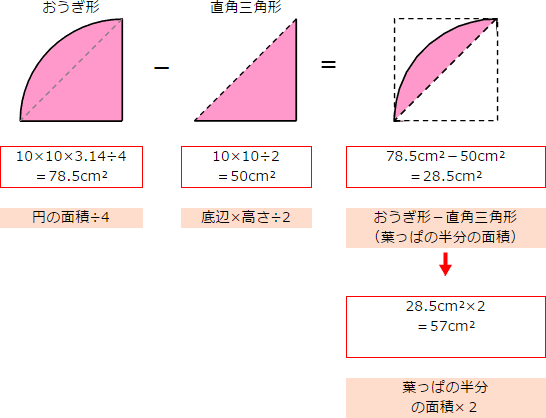



面積の求め方 算数の教え上手 学びの場 Com
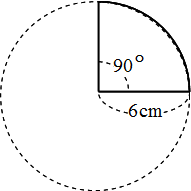



世界一やさしい 円の面積を求める問題の解き方 働きアリ
で習った円の面積の公式 円の面積= π £(半径)2 より得られるので、その求め方を思い出しその際にlim θ!0 sinθ θ = 1 を用いてい ることを確認する。 下図のように半径r の円を上下で切り離して2n 等分した扇形を交互に はめていく。正n角形の面積 円に内接や外接する正n角形の面積から円周率を求めます。 正2n角形の周りの長さ 円に内接2n角形の周りの長さの求め方 確率で円周率を求める方法 モンテカルロ法による円周率の計算 紙と鉛筆でπを求める方法 ビュッフォンの針(拡張版) 《円の直径の求め方》 円周=直径×314=4396 であることから この円の直径=4396÷314=14(cm) 答え 14cm




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ



円周の求め方と円の面積について アタリマエ
円の面積の求め方を考える 円の面積 は π r2 、つまり、π× r × r で求められるのをご存知でしょう。円周率(えんしゅうりつ、英 Pi 、独 Kreiszahl )とは、円の直径に対する円周の長さの比率のことで 、数学定数である。 通常、ギリシア文字 π で表される。 円の直径から円周の長さや円の面積を求めるときに用いる 。 また、数学をはじめ、物理学、工学といった科学の様々な理論の計算式に球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) \(\displaystyle \frac {6}{D \rho}\) 半分以上隠れている円の直径の推定 接触角の概算 円と球の空間



問題93おうぎ形の面積




はっぱ型 の図形の面積 身勝手な主張
円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314 小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色(かげ)がついた部分の面積の求め方全体白い部分円の面積は 半径×半径×π が一般的です。 しかし以下のように考えることもできます。 直径×直径 = (半径×2)× (半径×2) = 半径×半径×4 つまり




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ
あなたの眼の前にそこそこいいパソコンがあるなら, モンテカルロ サンプリング でπを求めましょう! (x, y) を,両方とも1から1の範囲でランダムに選択 x2 y2 を計算 x2 y2 ≤ 1 なら 1, x2 y2 > 1 なら何もしない(円の内にある点の数m) ÷(全部の点の数n) を円の面積と考えます。円の内にある 点かどうかは、円の内部の領域を表す 不等式(x2y2<1)を満たすかど うかで判断します。 したがって、π/4=m/n より、 π=4m/nで円周率が求められます。円の接線、おうぎ形の作図の練習や、円周率(π)を用いて円とおうぎ形の弧の長さや面積を求める練習、また、おうぎ形の中心角の求め方などを練習できる問題プリントです。 円とおうぎ形(1) 答え 円とおうぎ形(2) 答え 円とおうぎ形(3) 答え



P 3 05を証明せよ 東大の伝説の入試問題をプログラムで解く 組み込みエンジニアの現場力養成ドリル 27 3 5 ページ Techfactory



盲点の英単語 その8 円の面積の求め方を英語で言える 中学の英語をあなどってはいけない
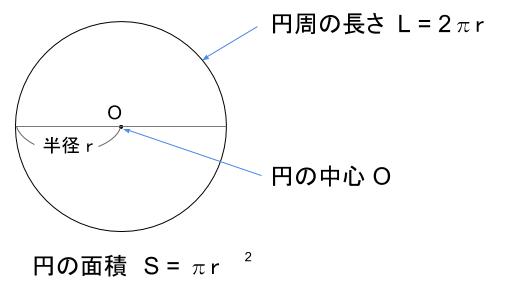
面積の求め方 扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 また、2行目の l は扇形の円の面積から円周(Circumference)を計算する 円の面積から円周を求めるには √ ( 面積 ÷ π ) で半径(r)を求め、 半径(r) × 2 × π で求めることができます。 ・底面の円の面積は 3×3×π=9π㎡ ・高さは 8cm よって、求める円柱の体積は、9π×8=72π㎥ 中学生になると、円周率πを使えて「 ×314 」の計算をしなくて良い場合が多くなって楽になりますが、文字式のルールに従った書き方をしましょう。



円の面積の公式 この問題をやれば円の面積は余裕だぜ 三重の個人契約家庭教師
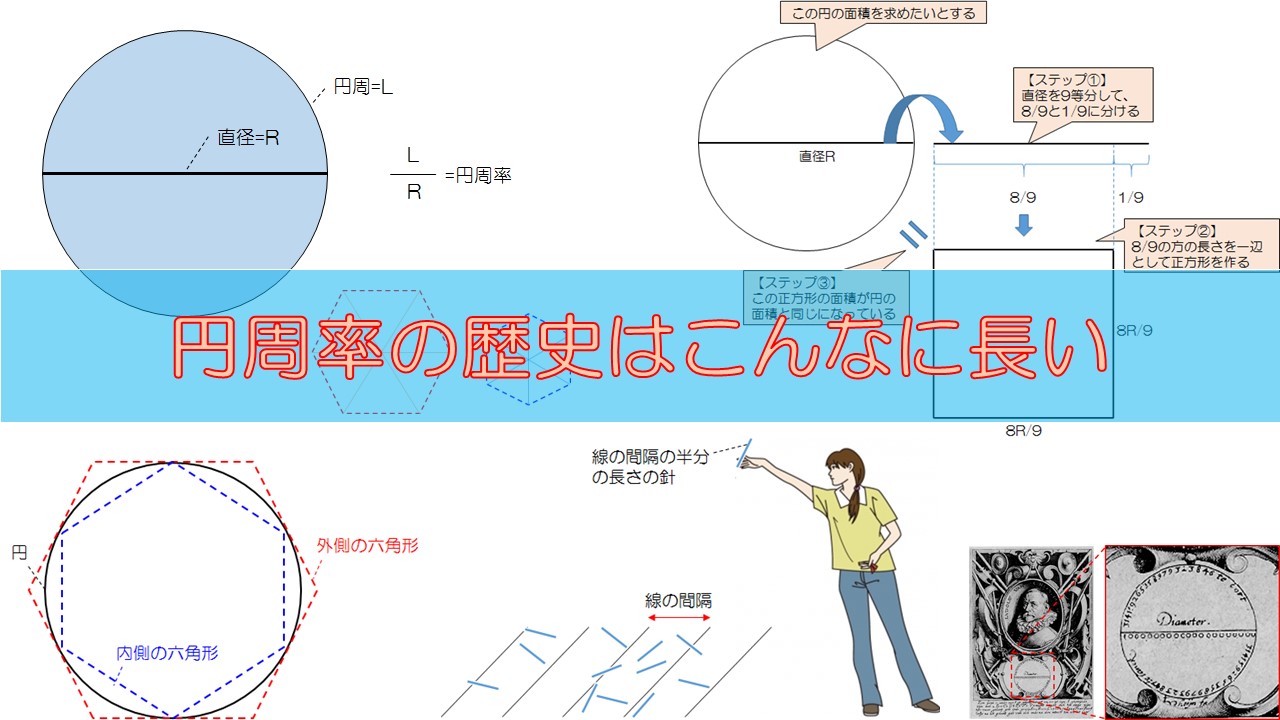



面白い円周率の歴史 昔の人たちはこうやって3 14 を求めてた 数学の面白いこと 役に立つことをまとめたサイト
3 * 3 * で求められた円の面積が出力されているのがわかります。 また、半径 × 半径の部分は、半径の2乗であるため、Powメソッドを使用することができます。 この記事では、「円周率 \(\pi\)」の意味や求め方、\(100\) 桁までの覚え方をご紹介していきます。 また、円周率を使って円の面積や円周を計算する問題についても解説していくので、ぜひこの記事を通して知識を深めてくださいね! 円を扇形に切って並べ直してみると 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるの




円の周りの長さを計算しよう 家庭学習レシピ



乱数を使った円周率の求め方 東京工科大学 メディア学部 ブログ




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun




円の面積の求め方 公式と計算例



1




Newtonライト 円周率p ニュートンムック 本 通販 Amazon




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




円周率の記号 P 中1は円の復習の大チャンス たぬぬ塾 中学校の先生たち



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su



円の面積 円周の求め方 公式 小学生 中学生の勉強




円の面積 算数用語集




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




円の面積の公式 算数の公式



円周の求め方と円の面積について アタリマエ




円の面積の求め方 公式と計算例
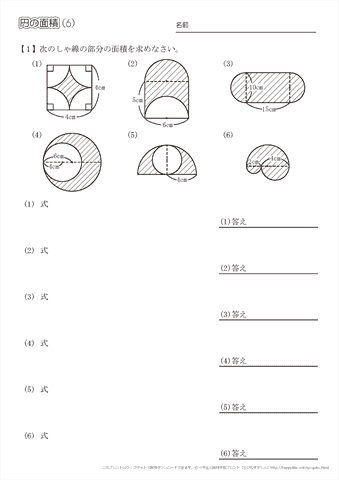



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
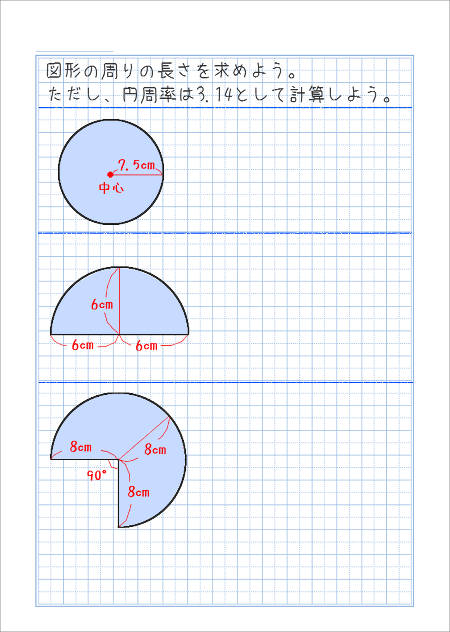



円の周りの長さを計算しよう 家庭学習レシピ




円の面積 練習応用 Youtube




直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ




標準 おうぎ形と正方形の面積 なかけんの数学ノート




円の面積の応用 小学校6年算数より 身勝手な主張



円の面積の求め方を教えてください 4分の1の大きさの円 です Yahoo 知恵袋
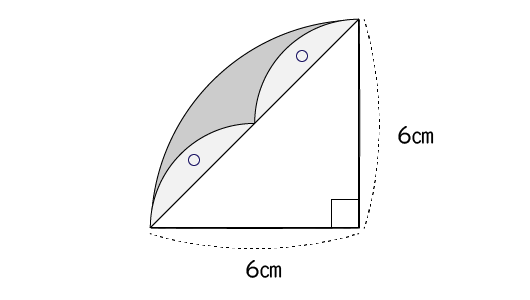



中学1年生数学 複雑な面積の求め方 長野地区 Itto個別指導学院 長野市の学習塾




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




半径 求め 方 ニスヌーピー 壁紙




小6 算数 小6 2 円の面積 応用編 Youtube




山と数学 そして英語 小学校算数 円の面積に関する応用問題



円周率 P とは 求め方や100桁までの覚え方をご紹介 受験辞典



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau




教えてください どうしても分からないんです 教えてください Clear



円の面積を 一般的に知られている公式を使わずに算出する方法を教えてくれませんか Quora



モンテカルロ法による円周率の計算



多角形の面積で円周率を求める Allisone




エクセルで円周率のpを使う 手っ取り早く教えて



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




この図形の面積の求め方を教えてくださいm M Clear



円の面積 算数の公式覚えてますか




中1数学 円周率 P について 例題編 映像授業のtry It トライイット




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
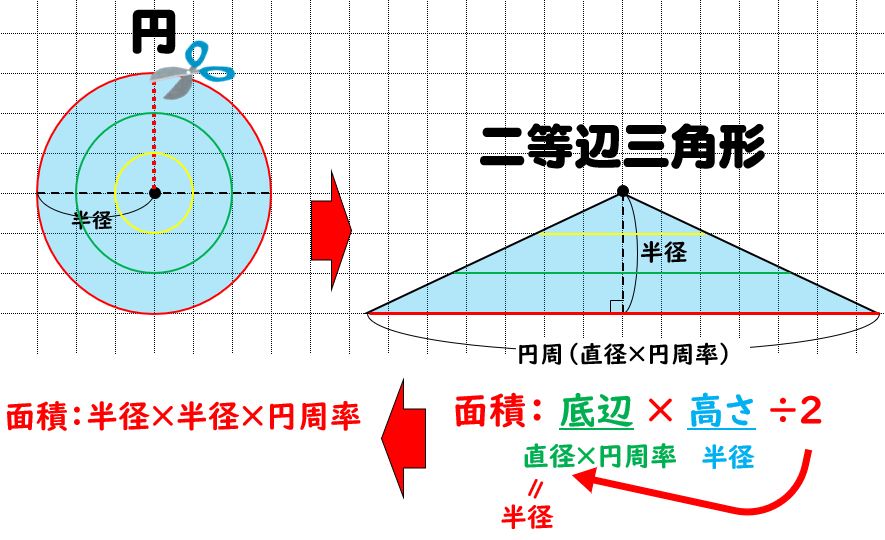



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




円周の求め方と円の面積について アタリマエ




Excel エクセルで円の面積から直径を計算したり 直径から面積を求める方法 Pi関数の使用方法




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト



工作4




扇形の面積の求め方 公式と計算例



6年算数 円の面積 2 わかる教え方



色のついた部分の面積を求めなさい ただし 円周率はpとします この問 Yahoo 知恵袋




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



円周率 P とは 求め方や100桁までの覚え方をご紹介 受験辞典
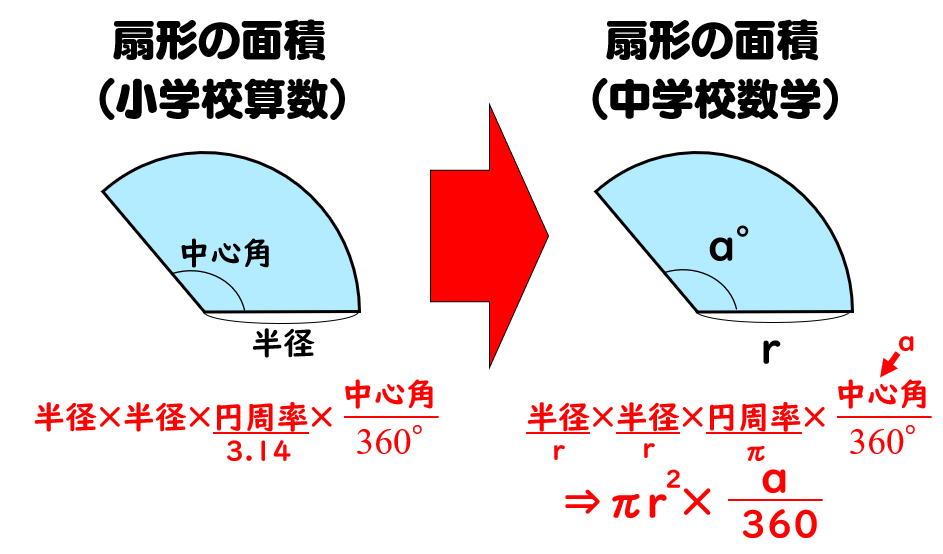



円 扇形 の面積 周や弧の長さの公式 数学fun




Excel エクセルで円の面積から直径を計算したり 直径から面積を求める方法 Pi関数の使用方法




小学生でもできる円周率の求め方 いろいろな方法を紹介 数学の面白いこと 役に立つことをまとめたサイト
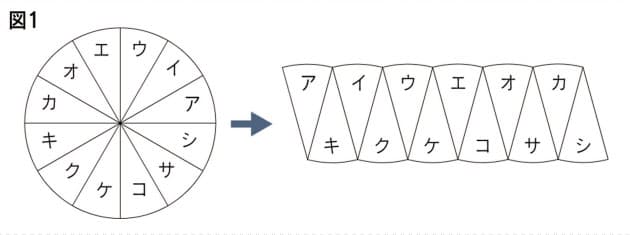



子供に説明できる 円の面積の公式 の証明 Nikkei Style



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素



250枚 至急 葉っぱ形の図形の面積について質問です Yahoo 知恵袋
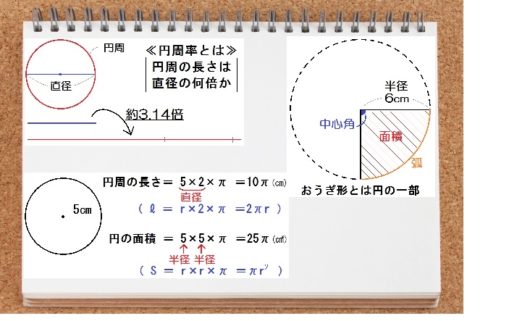



中学数学 平面図形 のコツ 円とおうぎ形




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく



Q Tbn And9gct8mjpenhvsxxfek Ceorhkk1e5jnkqcmelwl1yafnkyt4mflap Usqp Cau




円 扇形 の面積 周や弧の長さの公式 数学fun
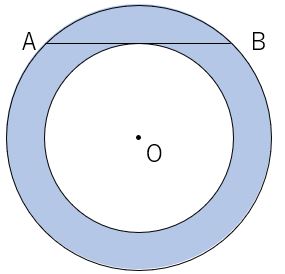



面積 円の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧




円の面積 円周の求め方 公式 小学生 中学生の勉強
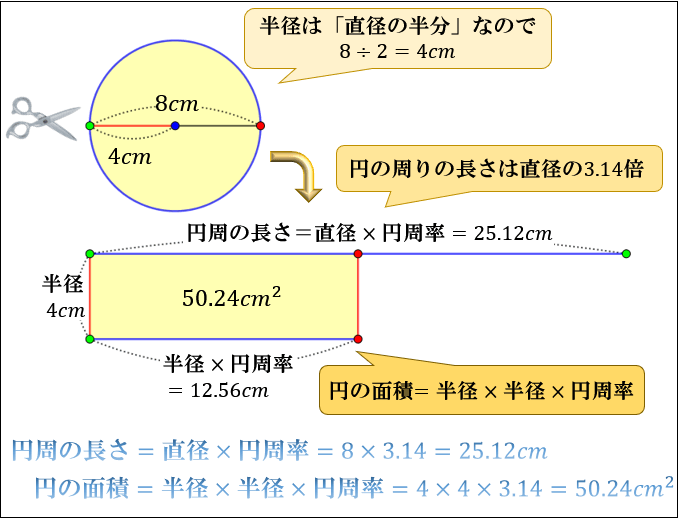



円周の求め方と円の面積について アタリマエ



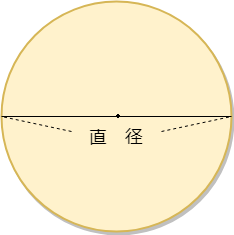
円の面積 直径




半円や4分の1の円 四分円 の面積を計算する方法 白丸くん



1
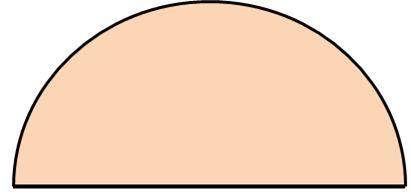



半円や4分の1の円 四分円 の面積を計算する方法 白丸くん
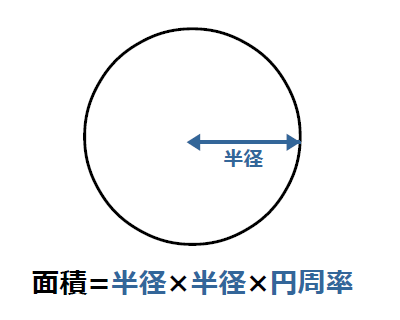



円の面積計算 ゆるゆるプログラミング




斜線の部分の面積を求めなさい 上の図は 半径10センチメートルの円の半 Okwave
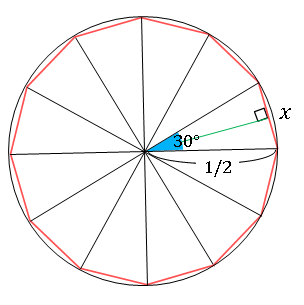



円の面積と周長
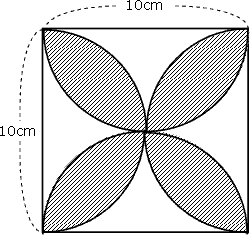



面積の求め方 算数の教え上手 学びの場 Com




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




円の面積の求め方 公式と計算例




円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張
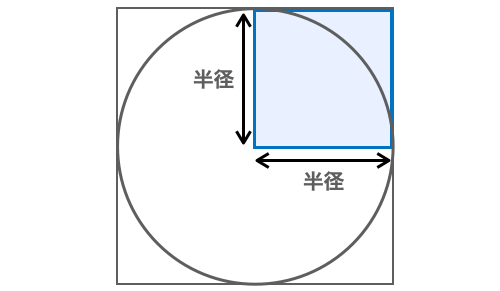



プログラミングで円周率を求める だえうホームページ




小6 算数 小6 旧 円の面積 Youtube




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく



内接多角形と外接多角形から円周率を求める




円柱の表面積と体積を求める公式 具体例で学ぶ数学
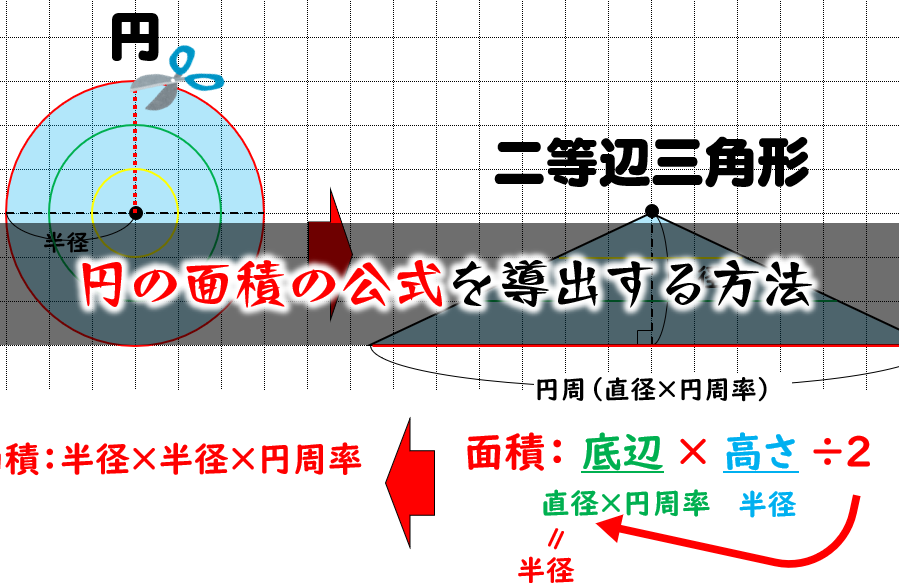



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




円の面積 円周の求め方 公式 小学生 中学生の勉強




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




円の面積の求め方 公式と計算例
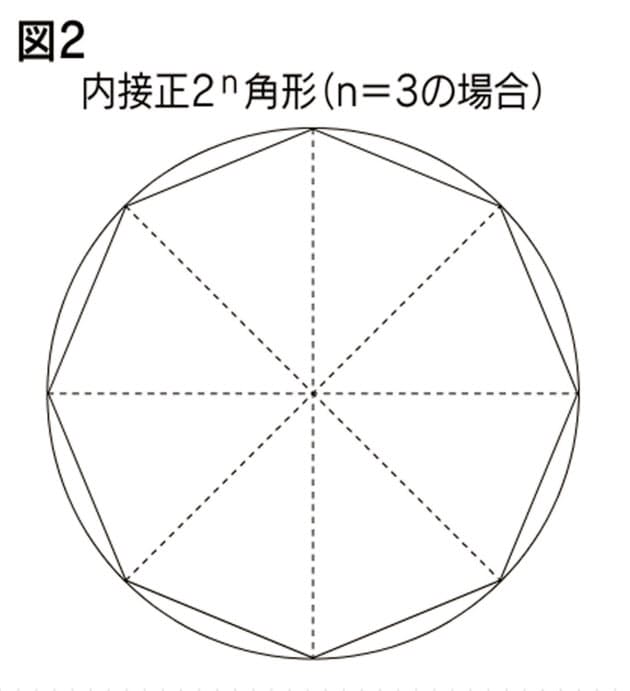



子供に説明できる 円の面積の公式 の証明 Nikkei Style




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ




円の面積 算数用語集


