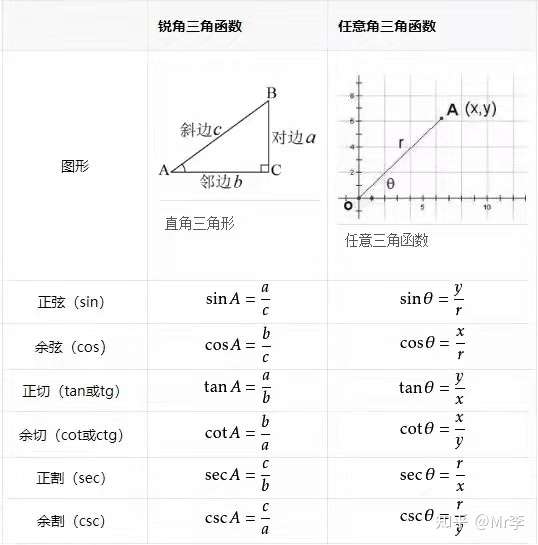
如果给出足够的几何属性,任意三角形计算器就能自动补全任意三角形的所有属性,例如面积,周长,边和角度。 三角形是具有三个顶点(角)和三条边(边)的多边形。 任意三角形 维基百科页面相关计算器:等边三角形计算器等腰三角形计算器直角三角形计算器直角三角形计算器 如果给出足够的几何属性, 直角三角形计算器 就能自动补全直角三角形的所有属性,如面积,周长,边和角度。 直角三角形是一个具有三个顶点(角)和三个边(边)的多边形,其中两条边以直角相交。 直角三角形 维基百科页面 三角比3|実は当たり前! ? 3つの (90°θ)型の変換公式 θ を扱ってきました. ( 90 ∘ − θ) を考えます. のような 角度が異なる三角比の計算はこのままでは難しいのですが,この記事で扱う ( 90 ∘ − θ) 型の三角比の変換公式を使うと計算ができます

Sin Cos Tan公式sin Yzkgo
三角比 角度 公式
三角比 角度 公式-高校数学Ⅰの「三角比」では、正弦定理と余弦定理がメインに出てきますよね。 でも、公式が多くて、全部覚えてたら頭がパンクしてしまいますよね。 三角比を攻略するには、sin cos tan の計算や正四 、用计算器的 tan1 键来求角度 Tan x° = 对边/邻边 = 300/400 = 075 tan1 of 075 = 369° (保留一位小数)



1
四、计算三角函数 上图中所有角度、所有线段长度都已经知道,根据三角函数的定义: 给分子分母同时乘以 ,可得: 这样我们就得到了: 知道了 sin18° 和 cos18° 之后,就可以根据三角函数的倍角公式、和差角公式推导出其他18°倍角的三角函数解析式。 1、公式一:设α为任意角,终边相同的角的同一三角函数的值相等 sin (2kπα)=sinα (k∈Z) cos (2kπα)=cosα (k∈Z) tan (2kπα)=tanα (k∈Z) cot (2kπα)=cotα (k∈Z) 2、公式二:设α为任意角,πα的三角函数值与α的三角函数值之间的关系 sin (πα)=-sinα cos (πα)=-cosα 三角函数公式 余切(cot)等于邻边比对边;cotA=b/a; 一般在解三角形中经常使用这些等式! 将一个角度拆成两个角之和或者差的形式
三角形 ,又稱三邊形,是由三條 線段 順次首尾相連,或不共線的三點兩兩連接,所組成的一個閉合的平面圖形,是最基本和最少邊的 多邊形 。 一般用大寫英語字母 A {\displaystyle A} 、 B {\displaystyle B} 和 C {\displaystyle C} 為三角形的 頂點 標號;用小寫英語字母E三角函數角度的變換法則 (1) 象限 第二象限 第三象限 第四象限 角度變 換公式 180 °−θ或90°θ 180°θ或270−θ 360°−θ或270°θ (2)凡角度遇到180 °±θ或360±θ時,函數不需轉換 °(3)凡角度遇到90±θ或270°±θ時,函數需轉換 iesinθ↔cosθ;tanθ↔cotθ;secθ↔cscθ頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b
三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる:有一個角為直角的三角形稱為直角三角形。 在直角三角形中,直角相鄰的兩條邊稱為直角邊。 直角所對的邊稱為斜邊。 直角三角形直角所對的邊也叫作「弦」。若兩條直角邊不一樣長,短的那條邊叫作「勾」,長的那條邊叫作「股」 。 直角三角形滿足畢氏定理(勾股定理),即兩直角邊邊長的三角比の角度の公式をまとめたいと思います。 角度の公式といっているのは、θ 90°や90° θといった類のものです。 90° θ(0° = θ = 90°)のとき




三角学 Wikiwand




数学高中三角函数的温习 老花的博客 Csdn博客
三角形の辺の長さなどから角度(角の大きさ)を求める方法です。 次の2パターンに分けて説明します。 パターン1:3辺の長さから角度を求める方法 パターン2:2辺の長さと1つの角度から残りの角の大きさを求める方法 メインで活躍する公式は第二余弦 比平常的角度要大,不是常见的 最后再利用奇变偶不变 符号看象限求出相应三角函数值 2利用三角函数的诱导公式 例如sin23°×cos37°cos23°×sin37 一連の記事はこちら 三角比1|三角比を考え方から理解する!有名角の三角比も! 三角比2|sinθ, cosθ, tanθの超重要な4つの関係式 三角比3|実は当たり前!3つの(90°θ)型の変換公式 三角比4|角度が90°以上の三角比はこう考える! 三角比5|(180°θ)型の変換公式はめっちゃ簡単!




高中数学必修四 三角函数突破点 二 弧度制及其应用 每日头条
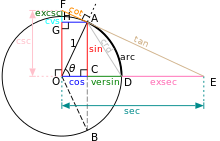



三角学 维基百科 自由的百科全书
今度は、正弦定理を利用して角度を求めていきます。 三角比の方程式の解き方を思い出しましょう。 今回は、角度の範囲について注意が必要です。 解答 正弦定理より であるため、 ここで A = 60º より 0º < B < 180º A = 1º であるため B = 45º また C三角形の面積公式を使うためには、2辺と間の角が必要になります。 なので、角Aの部分を使って計算を進めていきます。 角Bを使って面積を求めたければ 辺 の長さが必要になりますね。 このように与えられた情報から、どの部分を使えばよいのかを自分直角三角形の定義とさまざまな公式 レベル ★ 基礎 平面図形 三角比・三角関数 更新日時 直角三角形 とは,1つの角が直角である三角形のことです。 直角三角形のさまざまな性質を紹介します。 目次 三平方の定理(ピタゴラスの定理)




三角函數 機械學習相關問題 隨意窩xuite日誌




適切な三角形角度公式
电线以 68°的角度连到杆端。 电线有多长? 一、两条边是 对边(70)和 斜边(w)。 二、从上面的公式,我们知道应该用 正弦。 三、写下正弦的比: sin 68° = 70/w ;三角比に慣れてきた人のために 上にあげた「サインとコサインを2乗して足すと1」という公式は、実は三平方の定理そのものです。 三角比とは、形を変えた三平方の定理といえます。 三平方の定理をもう少しわかりやすく、使いやすくするためにサイン 三角関数の2倍角の公式・半角の公式の証明と応用 スポンサーリンク 高校数学Ⅱ 三角関数 検索用コード 証明は容易で,\ \bm {加法定理において\ \beta\ →\ \alpha\ }とするだけである \bm {利用機会が極めて多い}ので,\ 毎回加法定理から導くというのは



三角函数两角和差公式推导 初三网




每周一点canvas动画 三角函数 Segmentfault 思否
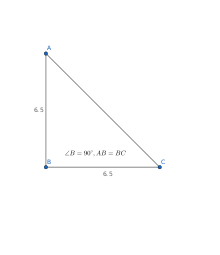
直角三角形计算 直角三角形在线计算器 请在下面输入数值 (图形在下面) a垂直边长 b底边长 c斜边长 A角度 B角度 C角度 三角比・三角関数を総まとめ! 定義や各種公式重要記事一覧 21年2月19日 三角比・三角関数に関する様々な公式をまとめていきます。 詳細記事へのリンクも載せていますので、ぜひ勉強の参考にしてくださいね! 目次 非表示 三角比・三角関数の多角 (3A) 与角 A 的三角比 直角三角形中角的三角比定义了角与其边长之间的关系。 sin 3x 或 cos 3x 等也是一种这样的三角公式,也称为三重角公式,因为它有一个三重角。 (1) sin 3A = 3sin A – 4 sin 3 A 证明: 让我们以 LHS 罪 3A = 罪 (2A A) 使用身份




一张图记住余角和补角的三角函数 知乎



三角函数公式 百度经验
底辺と高さから角度と斜辺を計算 1985年に紙の資料に描かれた複数の図をCADで製作する際に使用しました。 とても便利で業務を行う上で大変助かりました。 ありがとうございます。 オリンピックのブルーインパルスの展示飛行は高度1500m。 Googleマップで球面三角法の基本公式 abc を球面三角形とし辺 bc, ca, ab の長さをそれぞれ a, b, c とする。弧 ab を含む大円が乗る平面と弧 ac を含む大円が乗る平面のなす角を a とする。これは、点 a における2つの大円の接ベクトルのなす角ともいえる。< 鈍角の三角比1 > 角度θが90 以上の場合の三角比を 次で定める。 正の数r に対し,点Q(r,0) を原点 O(0,0) を中心として反時計まわりに角 度θだけ回転した点をP(X,Y) とする。 このとき角度θにおける三角比を sinθ= Y r, cosθ= X r, tanθ= Y X で定める。




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




三角形 08 直角三角形內角的基本計算題2 Youtube
三角比を用いた代表的な計算問題をマスターしましょう。この記事では「様々な三角比の四則演算」「等式を証明するもの」「sin, cos, tan の値を計算するもの」「式の値を計算するもの」についてまとめました。本記事で取り上げた問題はどれも定期試験頻出。 30°、45°、60°の三角比の値 これまでは直角三角形の辺の長さを比べながら三角比の値を求めてきました。 先ほどの問題で実感した通り、3つの辺の長さを求めないと三角比の値が分かりませんでしたね。 しかし、この章のタイトルにあるように 数学4-2 2) 負角、余角、補角の式変換 三角比を含む計算問題の中には、sinθやcosθの「θ」の部分が複雑なものになっているときがあります。 具体的には、sin (-θ)やcos (π/2-θ)、sin (π-θ)といったようなものが挙げられます(ほかにも色々あります




Sin Cos Tan公式角度sin Qaxnl
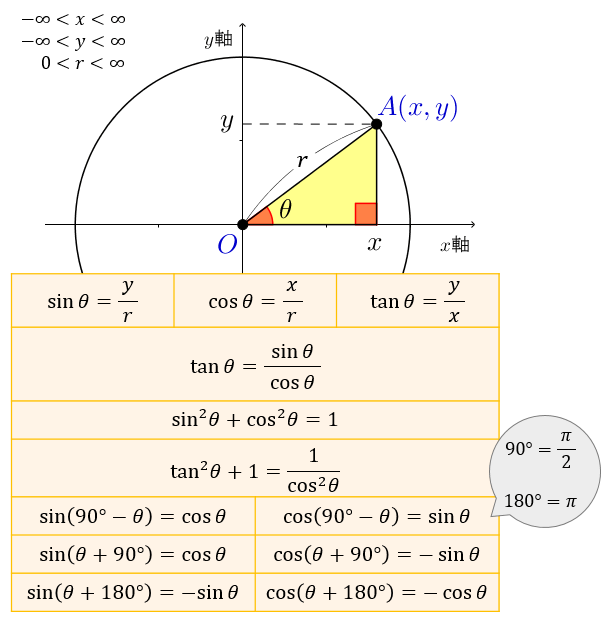



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




基礎三角比 Youtube
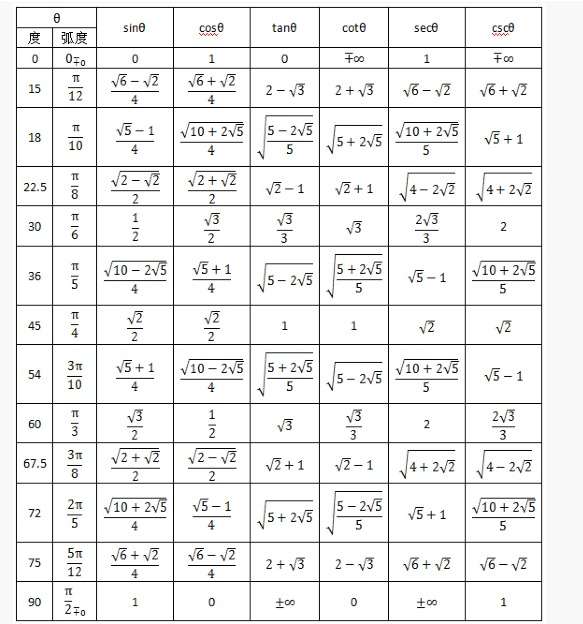



最全三角函数公式推导 知乎



考生必记 三角函数公式汇总 记忆 没有比这更全 知乎




高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト



三角法



三角形 维基百科 自由的百科全书



三角斜边计算公式图解 万图壁纸网




如何计算角度 8 步骤 包含图片




實用的三角函數值對照 每日頭條




余弦定理で角度を求める方法 数学の星




正弦公式的計算 1 Youtube




初学数控车床 这三角函数计算公式 收藏随时用 网易订阅




直角三角形知道两边求角度 中考数学专题复习 直角三角形 雪灵谷自然地理的博客 Csdn博客




如何计算角度 8 步骤 包含图片



直角三角形的斜边计算公式求三角形斜边长公式 朵拉利品网




02特殊角的三角函数直角三角形的边角关系初中数学初三 Youtube



三角函数 玄数




三角函数 正弦余弦定理及应用 羊羊的博客 程序员宅基地 正弦公式 程序员宅基地



初中 彻底度量345三角形 345三角形的精确角度 精作网



坡度计算公式坡度和角度计算公式 银颜网




三角比を用いた計算問題をマスターしよう スタディクラブ情報局



Tan半角公式推导过程三角函数半角公式的推导 朵拉利品网



三角形中三角比的特殊公式 知乎




三角恒等式 维基百科 自由的百科全书
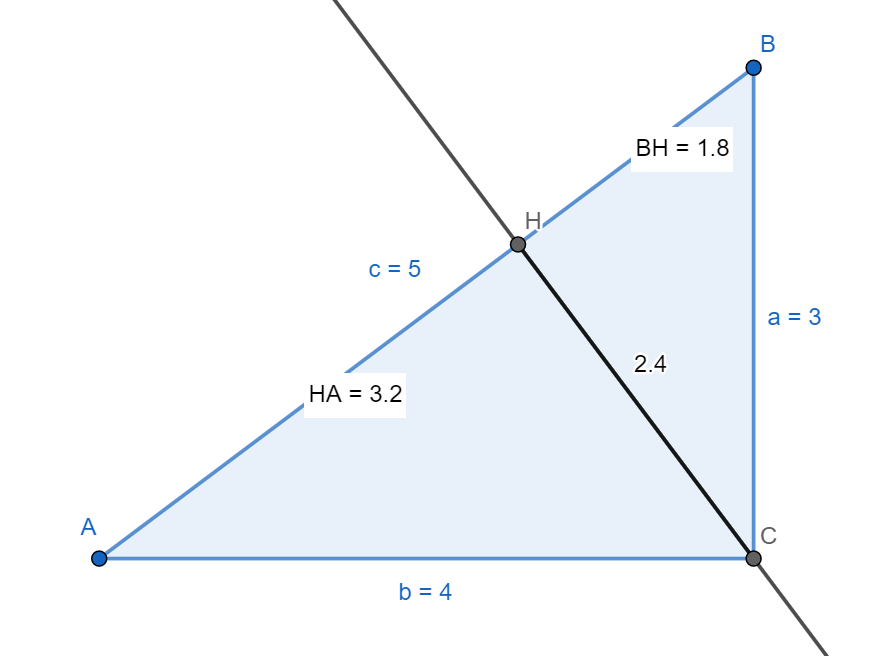



初中 彻底度量345三角形 345三角形的精确角度 精作网




如何 Excel Tan功能 查找角度的切线 21
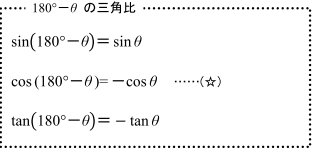



180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座



3



少有人走的路 三角函数超入门 2 锐角三角形的三角比
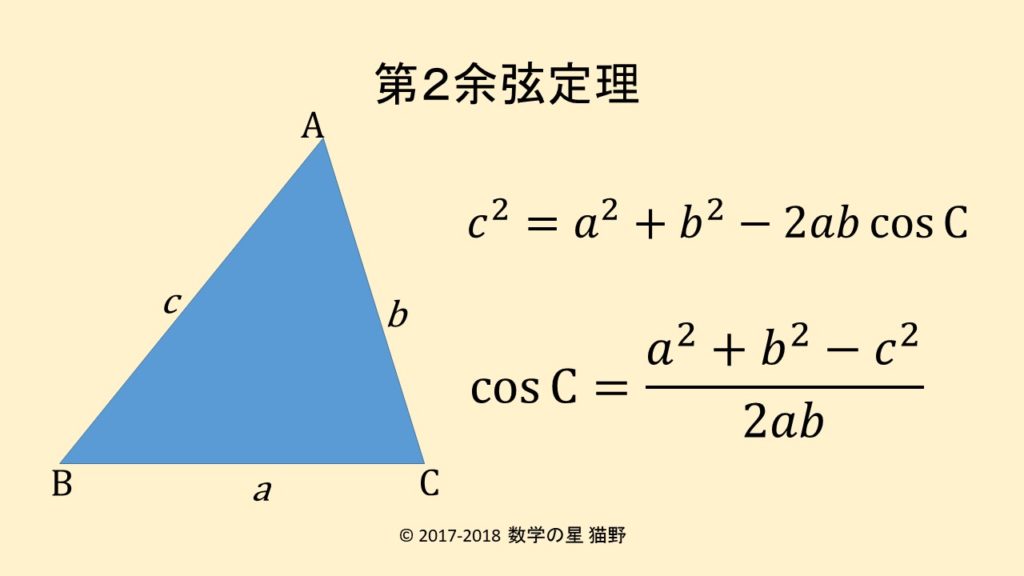



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星




Sin Cos Tan公式角度sin Qaxnl




正弦 余弦和正切



三角形三边与角度公式 西瓜视频搜索
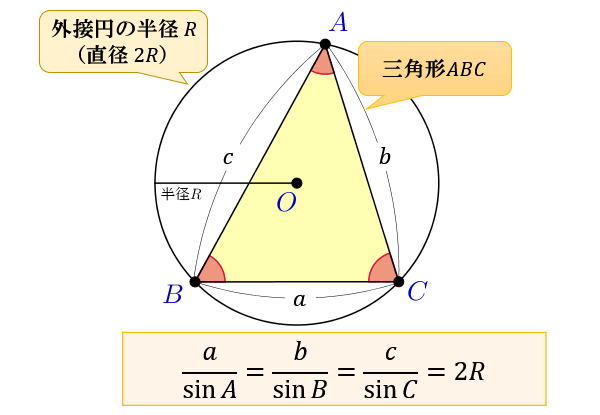



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ



高中三角函数公式推理 记忆 知乎




三角函数公式 Jack Meng 博客园



坡度计算公式坡度和角度计算公式 银颜网



三角函數基本概念



1




Sin Cos Tan公式sin Yzkgo




高中生必备实用三角函数公式总表 数学提分有妙招 建议看 楠木轩



直角三角形斜边直角三角形求斜边长计算公式 朵拉利品网



1



達人專欄 一篇文弄懂三角函數 其實它真的不可怕 Johnny的創作 巴哈姆特




Sin Cos Tan公式sin Yzkgo




三角函數 機械學習相關問題 隨意窩xuite日誌




三角恒等式 维基百科 自由的百科全书
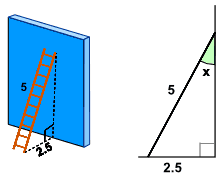



求直角三角形的角度




廣義角轉換成銳角之法則 Youtube




如何计算角度 8 步骤 包含图片




正弦 余弦和正切




Sin 求角度 Sin求角度



Tan公式 万图壁纸网




如何计算sin1 等于多少 星火网校




三角函数公式 Jack Meng 博客园
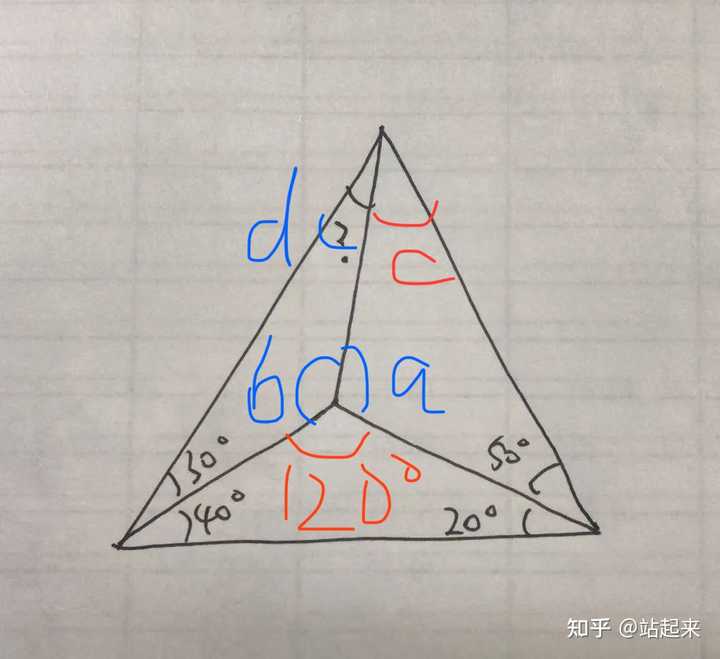



求三角形内角度数公式 三角形角度计算公式 求出三角形各角的度数



三角函數和角差角公式之幾何圖解與記憶口訣 創意海豚的部落格 Udn部落格



三角形三边与角度公式 西瓜视频搜索
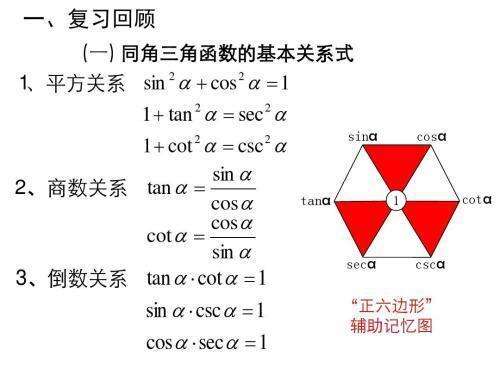



任意角的三角函数与诱导公式 熟练记忆透彻理解 就在这些口诀上 楠木轩
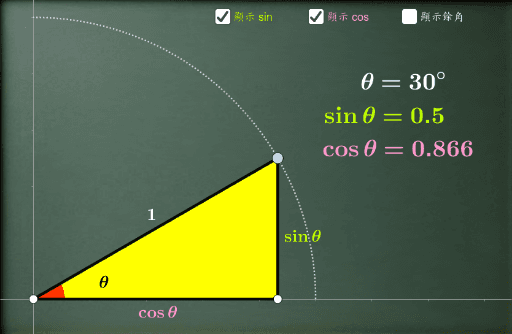



三角 Geogebra



三角形边长公式和图解 信息评鉴中心 酷米资讯 Kumizx Com



三角函数cos是什么边比什么边 初三网



達人專欄 一篇文弄懂三角函數 其實它真的不可怕 Johnny的創作 巴哈姆特



5直角三角形的边角关系之特殊角总结 哔哩哔哩 つロ干杯 Bilibili




わかりやすい三角比と基本公式 Irohabook




三角形角度計算機任意三角形求角度計算公式 Wjklv




11 3 三角函数 Acionscript3 0 教程



1



三角函数公式转换大全图解三角函数公式 有途教育



初中三角形角度计算方法 三角形斜边长度怎么算 求三角形边长公式




求直角三角形的角度




初中三角函数公式表格 初中三角函数公式表 三人行教育网 Www 3rxing Org




Sin Cos Tan数值表是以角度 数学上最常用弧度制



三角函数度数公式图片 信息评鉴中心 酷米资讯 Kumizx Com



高中数学二倍角公式 图片欣赏中心 急不急图文 Jpjww Com




三角形面積公式 兩邊一夾角 Youtube



三角形角度公式 ニスヌーピー壁紙
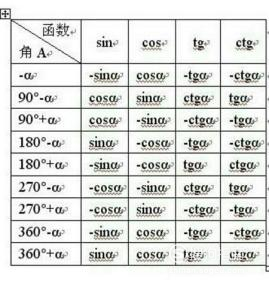



常用的三角函数公式集合三角函数公式整理 Iiiff互动问答平台



三角函数指数 高一数学公式三角函数角度对应表 尚书坊




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




三角函數 維基百科 自由的百科全書



三角函數基本概念




三角函数公式初中图解



三角形三边与角度公式 西瓜视频搜索




三角形角度计算公式利用计算器上的反余弦函数功
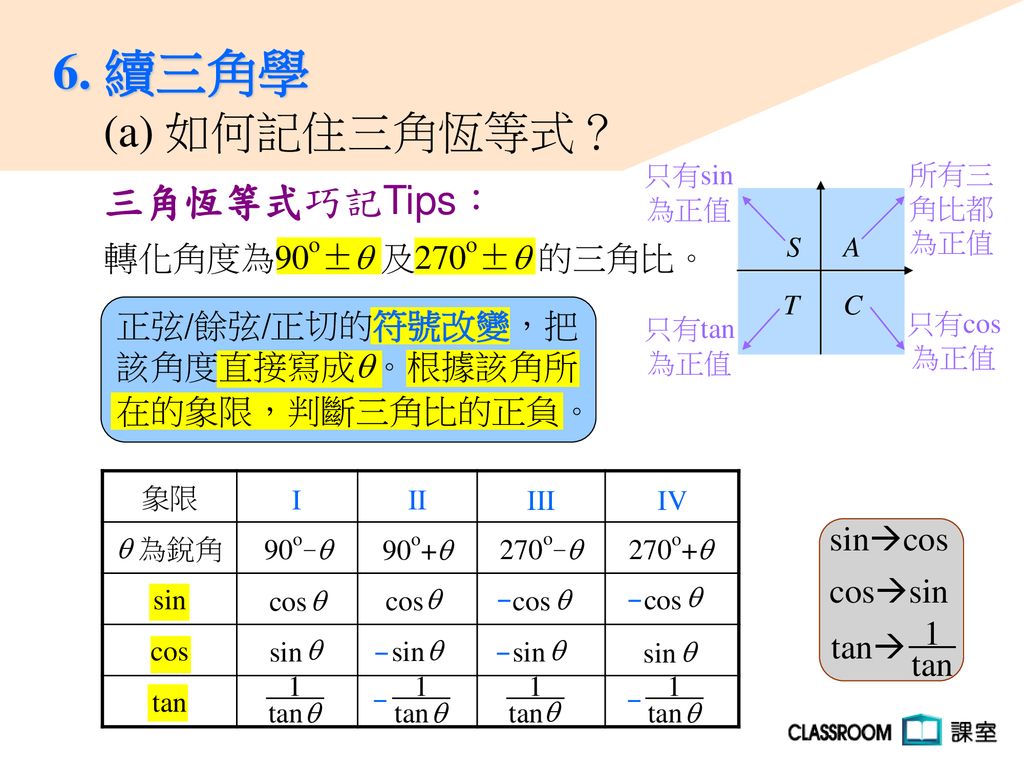



6 續三角學 A 如何記住三角恆等式 三角恆等式巧記tips 轉化角度為180o 及360o 的三角比 Ppt Download




如何计算角度 8 步骤 包含图片
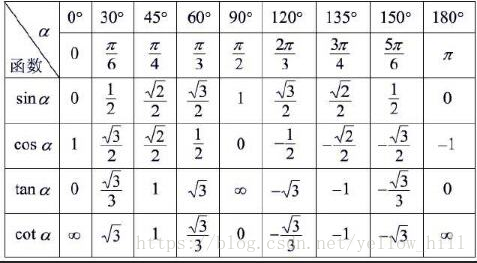



最常用的三角函数值和三角变形公式 山云的专栏 Csdn博客 三角函数值




三角函数公式 百度经验


